Can an idea from 1927 still shake the foundations of modern physics? The pilot-wave theory, first proposed by Louis de Broglie, suggests that particles follow precise paths, guided by a real wave—a notion that radically differs from standard quantum mechanics. For decades, this theory was pushed aside as a fringe interpretation. But today, it’s experiencing a renaissance, drawing interest from physicists, philosophers, and mathematicians alike. Could this be the bridge between determinism and quantum uncertainty?
A Forgotten Path at the Heart of Quantum Mechanics
When de Broglie introduced his pilot-wave model in 1927, quantum mechanics was still young and unsettled. His core idea was deceptively simple: what if particles, like electrons, were not just probabilistic wave functions, but actual objects with real trajectories, guided by a wave field? He called this the pilot wave—a kind of quantum steering mechanism.
At that year’s famous Fifth Solvay Conference, where giants like Einstein, Bohr, Heisenberg, and Schrödinger debated the new science, de Broglie’s theory was met with skepticism. Bohr’s Copenhagen interpretation, which embraced indeterminacy and the probabilistic collapse of wave functions, quickly became the dominant narrative. De Broglie, under pressure, eventually abandoned his idea.
Yet he was planting a seed.
Bohm’s Resurrection: A Deterministic Turn
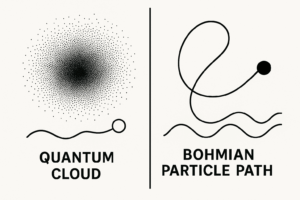More than two decades later, David Bohm picked up the pilot-wave thread. In 1952, he published a reformulated version, often called Bohmian mechanics¹. He showed that if you assume particles have real positions and are guided by a wave function evolving according to Schrödinger’s equation, you recover all the predictions of standard quantum mechanics.
In Bohm’s view, the particle is like a surfer, and the wave function is the ocean beneath. The wave evolves according to known physical laws and informs the particle how to move—but crucially, the particle’s position is never probabilistic. It always has a well-defined location, even if we can’t measure it.
This interpretation reintroduces determinism into quantum theory. It avoids the so-called measurement problem, in which a particle’s behavior seems to change depending on observation. In Bohmian mechanics, nothing “collapses”—everything is always in motion, always real.
The Elephant in the Room: Nonlocality
However, Bohm’s model does not come without controversy. One of its key features is nonlocality: the idea that a particle can be instantaneously affected by something happening to another particle, regardless of the distance between them. This was famously dubbed “spooky action at a distance” by Einstein.
In standard quantum theory, this kind of entanglement is deeply mysterious but accepted as a mathematical consequence of the formalism. In Bohmian mechanics, it becomes physical: one particle’s properties can truly depend on another’s, even across galaxies.
This makes Bohmian mechanics explicitly nonlocal, violating the principle of locality enshrined in relativity. That’s a major reason many physicists found it uncomfortable—even if it works.
Yet, experiments like Bell tests have shown that any realistic theory must be either nonlocal or non-realistic. Bohm chose realism. Mainstream quantum mechanics chose indeterminacy.
What Makes Pilot-Wave Theory Appealing Today?
Despite its determinism and nonlocality, the theory is gaining traction again. Why?
- Conceptual clarity: Bohmian mechanics offers an intuitive picture of what’s “really happening” at the quantum level. You can actually draw trajectories. In contrast, the Copenhagen interpretation is conceptually vague: particles exist as wave functions until observed, but what is “observation”? And when does the collapse happen?
- Measurement problem: Bohm’s theory bypasses the observer altogether. There is no magic moment where reality is decided. Everything simply evolves.
- Quantum computing & information: As research in quantum foundations becomes more relevant to practical technologies, interest grows in exploring alternative models of quantum behavior—including deterministic and hidden-variable approaches.
- Emergent behavior: There is increasing interest in theories where quantum behavior emerges from a deeper level of reality, possibly involving hidden variables or deterministic processes. Bohm’s theory fits naturally into this paradigm.
Fluid Analogies: Walking Droplets and Macroscopic Quantum Mimicry
In 2006, researchers Yves Couder and Emmanuel Fort demonstrated that bouncing droplets of oil on a vibrating fluid bath could mimic quantum-like behaviors². The droplets generated surface waves which, in turn, guided the motion of the droplets themselves. These analogues exhibited interference, quantized orbits, tunneling, and even memory effects.
While these are not true quantum systems, they offer visual analogies to the kind of trajectory-wave duality Bohm described. In a pilot-wave model, a particle’s path is determined by the wave’s configuration—and this is exactly what these droplets seem to do.
Though not direct evidence of Bohmian mechanics, such systems provide a powerful intuition for how quantum behavior might emerge from deterministic laws.
A Legitimate Theory—But Not the Only One
It’s important to note that Bohmian mechanics is not in conflict with quantum mechanics—it is mathematically equivalent to it in all standard predictions. However, it is an interpretation, not a separate theory in the predictive sense.
This raises a philosophical question: if it makes no new predictions, why care?
The answer lies in interpretive power. Science is not just about prediction; it’s also about understanding. Different interpretations offer different insights into what reality is, not just what it does.
Still, Bohmian mechanics faces challenges:
- Extending it to quantum field theory is mathematically difficult.
- Incorporating relativity in a fully consistent way remains an open problem.
- It’s nonlocal and deterministic in a world where randomness and locality seem deeply ingrained.
But these are not fatal flaws. They are frontiers.
Philosophical Consequences: Does Reality Need a Pilot?
Pilot-wave theory reopens age-old debates: Is the universe deterministic? Does consciousness collapse the wave function? Are we fundamentally misinterpreting the mathematics of quantum theory?
Bohm believed that the universe was an undivided whole, and that the pilot-wave was part of a deeper implicate order—a hidden layer of reality that gives rise to observable phenomena. This view is echoed in modern ideas about holography, quantum gravity, and even panpsychism.
Whether or not Bohm’s metaphysics hold water, the fact remains: the standard view of quantum mechanics is not the only game in town. And in an age where physics is seeking deeper unification, alternative interpretations like the pilot-wave model may have a crucial role to play.
TL;DR
- Pilot-wave theory suggests particles have real positions, guided by a wave field—a deterministic alternative to standard quantum mechanics.
- David Bohm resurrected the idea in the 1950s, introducing nonlocality and realism.
- Although it makes no new predictions, the theory offers conceptual clarity and bypasses the measurement problem.
- Modern interest is growing due to quantum computing, analog experiments, and foundational physics.
- While challenging to extend to quantum field theory or relativity, pilot-wave models remain a serious contender in quantum interpretation.
References
- Bohm, D. (1952). “A Suggested Interpretation of the Quantum Theory in Terms of ‘Hidden Variables’.” Physical Review, 85(2), 166–179. https://journals.aps.org/pr/abstract/10.1103/PhysRev.85.166
- Couder, Y., Fort, E. (2006). “Single-Particle Diffraction and Interference at a Macroscopic Scale.” Physical Review Letters, 97(15), 154101. https://doi.org/10.1103/PhysRevLett.97.154101
- Goldstein, S. (2017). “Bohmian Mechanics.” The Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/entries/qm-bohm
- Holland, P. R. (1993). The Quantum Theory of Motion. Cambridge University Press.
- Valentini, A. (2002). “Signal-Locality, Uncertainty, and the Subquantum H-Theorem.” In: Chance in Physics. Lecture Notes in Physics, vol 574. Springer.
- Bricmont, J. (2016). Making Sense of Quantum Mechanics. Springer.
Discussion
If quantum mechanics can be explained deterministically through hidden variables—why has the world embraced indeterminacy for so long?
